Ｒｙｎのページ（商業高校情報教育研究室）

待ち行列

例えば、 イベント会場で生ジュースを販売するとする。
私が、客から注文を受け、生ジュースを作り、会計をして商品を渡すまでに、 平均して４分かかるとする（平均サービス時間Ts）。
また、イベント当日は、客は平均して６分に１人やって来ると推測されている（平均到着間隔Ta）。
この場合の利用率（ρ＝Ts÷Ta）は４分÷６分≒０．６７となるが、
例えば気温が上昇し、客が平均５分に１人やって来るとすると、４分÷５分＝０．８、
平均４分に１人やって来るとすると、４分÷４分＝１、となり、
私１人で対応するには、非常に苦しくなる。
勿論、実際には、 私は毎回きっちり同じ時間でお客さんに対応出来ないし（大量だったり疲れたりとか）、 客がきっちり等間隔で到着するなんて事は有り得ない（昼食時には殺到したりとか）ので、 友人に声を掛けて手伝って貰って、 ジュース作成と会計など作業を分担し１人の客に対するサービス時間Tsを短縮したり、 客に対する窓口を増やしたり、といったことが必要となる。 後者の方式では、さらに、待っている行列を窓口ごとに作るか、 行列を１つだけにして空いた窓口へ振り分けるか、というパターンがある。

客の平均到着間隔Ta＝６分、私の平均サービス時間Ts＝４分という上記の例では、言い換えれば、
客は１時間に平均１０人やって来ると考える事が出来（平均到着率λ）、
私は１時間に平均１５人の客に対応出来ると言える（平均サービス率μ）。
参考書でよく見られる公式、利用率（ρ＝λ÷μ）は、これを用いる。

面倒くさい数式をぶっとばして、乱暴に結論だけ書くと、 一定時間に客が到着する人数の確率がポアソン分布、 店員がサービスをする時間の確率が指数分布に従い、 窓口が１つ、行列が１つ、の、Ｍ／Ｍ／１の待ち行列の場合、
行列で待っている人の平均人数 Lw は、
利用率÷利用していない率、ρ÷（１－ρ） 人で、
その待ち時間（注文をし始めるまでの時間）Twは、
待っている平均人数×１人にかかる平均時間、ρ÷（１－ρ）× Ts で求める事が出来る。
ρが０．５を超えると行列が出来、１を超えると行列は永遠に伸び続ける。

待ち行列で言うところの ポアソン分布と指数分布というこの２つの分布は表裏一体で、大雑把に言うと、 ポアソン分布は、ある事柄が一定の時間内に起きる確率を、 指数分布は、ある事柄が起きる時間の間隔の確率をあらわしている。 例えば、１時間に平均λ人の客が来るとすると、 １時間にｘ人の客が来る確率を求めるのがポアソン分布で、 客が来たｘ時間後に次の客が来る確率を求めるのが指数分布である。
EXCELには、ポアソン分布の POISSON() と指数分布の EXPONDIST() という関数があり、 シュミレーションをする事が可能である。

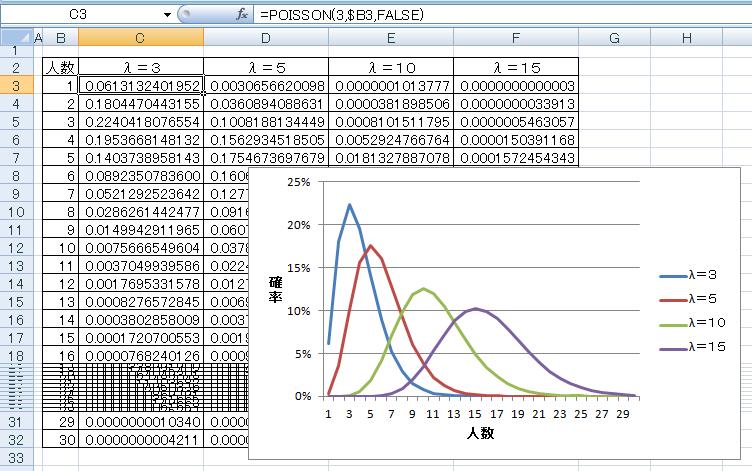
１時間に平均λ人の客がランダムに到着する場合、
左：１時間に到着する客の数がｘ人である確率。
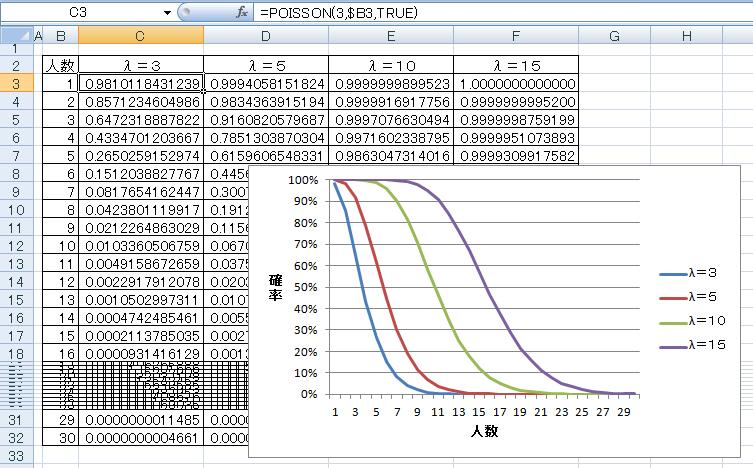
右：１時間に到着する客の数が少なくともｘ人である確率。


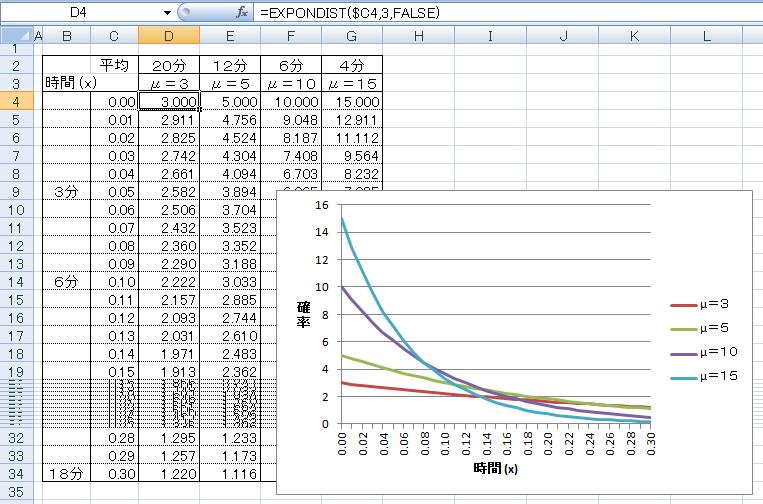
１時間に平均するとμ人の客にサービスする力がある店員の場合、
左：１人の客に対するサービス時間がｘ時間である確率。確率密度関数なので縦軸は１を超える。
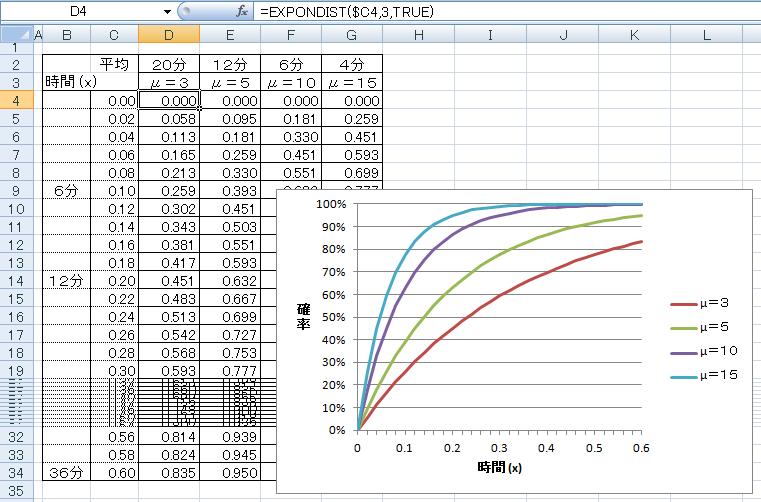
右：１人の客に対するサービス時間がｘ時間以内である確率。

---

「キーワード辞典」の目次へ