Ｒｙｎのページ（商業高校情報教育研究室）

浮動小数点数

コンピュータが扱うデータの形式の１つ。

数値を、（－１）^符号×仮数×基数^指数 の形で表現することで、整数だけではなく実数も含めて効率よく表現出来る様にしたデータ型。 浮動小数点数には幾つかの方法があるが、 最も一般的であるといわれているＩＥＥＥ７５４の３２ビット単精度の方法。

物凄く大雑把には、 コンピュータ内においてプログラムやデータを操作する際の単位を語（ワード）といい、 主記憶装置の各々の番地（アドレス）には一語が記憶出来る。 一語の大きさはコンピュータによって８ビット、１６ビット、３２ビット、など、色々ある。
また、プログラム言語のデータ型には様々な種類とその為に必要な大きさがある。 例えば、一語が１６ビットのコンピュータＣＯＭＥＴにおいて、３２ビットが必要なＩＥＥＥ７５４を使用する場合は、 １つのデータを記憶するために２語が必要となり、正しくデータを処理するための対応も必要となる。 ＣＯＭＥＴにそんな言語処理系が有るのかどうかは知りませんが。

ＩＥＥＥ７５４　３２ビット単精度

３２ビットのうち、

左端の水色の１ビットは符号部。正の数なら０、負の数なら１。

左から２ビット～９ビット目の緑色の８ビットは指数部。基数は２。
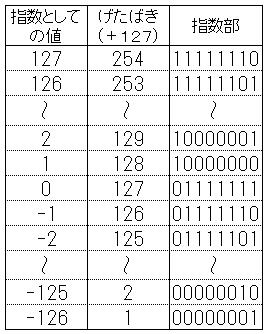
ビット列００００００００と１１１１１１１１は特別な意味を持つため指数としては使わない。 指数としての値は、十進数の－１２６から１２７までの範囲を扱う（プラスの方が多い）が、 二進数の補数によるマイナスの数の処理が面倒なため、 便宜上、指数としての値に十進数の１２７を加え、 全て符号なし二進数のプラスの値（十進数の１から２５４）にするイクシス表現であらわされる。 左図参照。

残りのオレンジ色の２３ビットは仮数部。
このデータ形式では、数値の符号は符号部で判るので、 より多くの値が扱える様に数値の絶対値を使う。
また、例えば二進数の１０１０は、 １０１０×２^０、１０１．０×２^１、 ０．１０１０×２^４、１０１００×２^－１、など、幾つもの表現が出来てしまい不都合なので、 整数部分は必ず１にして有効桁を最大限に使える１通りに限定し（これを正規化と言う。１．０１０×２^３となる）、 さらに、その整数部分は必ず１であることを了解事項として省略することで、実質２４ビット分を表現する事が出来る。

１０進数の－１１８．６２５という数値をこのデータ形式で表現する。

この値の絶対値である１１８．６２５を符号なしの２進数に変換する。
１１１０１１０．１０１
整数部分が１になる様にする（正規化）。
１．１１０１１０１０１×２^６
これを、あてはめていく。

数値の符号は負なので、符号部は、１。
指数部は、６に１２７を加えた１３３を二進数に変換して、１００００１０１
仮数部は、小数点以下の部分、１１０１１０１０１をあてはめ、残りのビットは０にする。

情報落ち

浮動小数点数で、 絶対値の差が極めて大きい値を加算する際に、細かい方の値がなくなってしまうこと。
面倒なので十進数、有効桁数が８桁の例。
１０００００＋０．００１＝１０００００．００１

桁落ち

浮動小数点数で、 殆ど等しい数値同士の減算を行った際に、有効桁数が減ってしまうこと。
面倒なので十進数、有効桁数が８桁の例。

√１００１－√９９９
＝３１．６３８５８４－３１．６０６９６１　（有効桁数同士の減算）
＝０．０３１６２３

解決法
（√１００１－√９９９）（√１００１＋√９９９）／（√１００１＋√９９９）
＝（１００１－９９９）／（３１．６３８５８４＋３１．６０６９６１）
＝２／６３．２４５５４５
＝０．０３１６２２７８１・・・
割り算なので、桁数が少なくならない。

---

「キーワード辞典」の目次へ